Découvrez Comment Rencontrer Une Équation Quadratique Avec Coefficients Entiers, En Sachant Que Ses Racines Sont, Et Maîtrisez Les Techniques De Résolution Efficaces.
**applications Pratiques Des Équations Quadratiques**
- Résoudre Des Problèmes De Trajectoire En Physique
- Calculer Les Maximums Et Minimums En Économie
- Modéliser Des Phénomènes Naturels Avec Des Équations
- Analyser Des Courbes De Croissance En Biologie
- Optimiser Des Ressources Dans Des Projets D’ingénierie
- Utiliser Les Équations Pour Prédire Des Événements Futurs
Résoudre Des Problèmes De Trajectoire En Physique
La physique regorge de concepts fascinants, mais peu d’entre eux sont aussi concrets que les problèmes de trajectoire. Imaginez un ballon projeté dans les airs, sa trajectoire formant une courbe parabolique. Pour comprendre ce phénomène, les équations quadratiques deviennent alors un outil indispensable. En utilisant la formule quadratique, on peut non seulement déterminer la hauteur maximale atteinte, mais aussi le moment où le ballon redescend. Dans ce contexte, ces équations sont comme des prescripteurs, nous guidant à travers les chemins des mouvements.
Ainsi, en étudiant le mouvement d’un projectile, on se rend compte que la clé réside dans l’analyse des points critiques. Ces points, où la trajectoire atteint son maximum ou son minimum, sont essentiels pour prédire le comportement de l’objet. Les physiciens utilisent des modèles basés sur ces équations pour simuler des scénarios variés, comme un athlète sautant par-dessus une haie ou une fusée s’élevant vers les étoiles. Comme une ordonnance bien définie, chaque équation incarne une solution vers une compréhension plus profonde des dynamiques en jeu.
Finalement, la capacité à prédire et à analyser ces trajectoires a des implications concrètes, que ce soit en ingénierie aéronautique ou dans les sports. En optimisant ces trajectoires grâce à des calculs précis, on peut réellement améliorer les performances et la sécurité. En somme, les équations quadratiques ne sont pas qu’un simple outil mathématique ; elles sont la clé d’un univers fascinant où chaque trajectoire raconte une histoire de mouvement et d’interaction.
| Éléments | Importance |
|---|---|
| Hauteur Maximale | Détermine le succès d’une trajectoire |
| Temps de Vol | Critique pour l’analyse des mouvements |
| Impact au Sol | Essentiel pour la sécurité des projets |

Calculer Les Maximums Et Minimums En Économie
L’analyse des maximums et minimums dans le domaine économique est essentielle pour maximiser le profit et minimiser les coûts. Lorsqu’une entreprise cherche à optimiser ses ressources, elle se tourne vers les équations quadratiques pour modéliser ses coûts de production. Par exemple, si une entreprise a des coûts proportionnels à la production, elle peut rencontrer des économies d’échelle dans une certaine mesure. En utilisant la méthode de dérivation, on peut localiser les points critiques où le profit atteint son maximum ou son minimum. Cela permet de déterminer le niveau de production optimal pour réaliser le meilleur bénéfice possible.
Grâce aux équations quadratiques, nous pouvons également examiner les interactions sur le marché. Imaginez une entreprise qui veut trouver le point d’équilibre entre l’offre et la demande. En établissant une équation où les revenus et les coûts sont équilibrés, les économistes peuvent déterminer à quel moment une entreprise devrait intervenir, afin d’éviter des pertes. Les graphes générés par ces équations offrent une visualisation claire des seuils critiques. Ainsi, la compréhension des extrêmes devient un outil crucial pour la prise de décisions.
En plus de ça, il est important de noter que les entreprises peuvent également utiliser ces concepts pour prévoir les tendances futures. En estimant les variations potentielles du marché, elles peuvent ajuster leurs stratégies. La capacité à encontre a equação quadrática com coeficientes inteiros sabendo que suas raízes são leur permet de naviguer efficacement dans un environnement en constante évolution. Les décisions basées sur des analyses quantitatives, intégrant les racines de ces équations, les aident à se préparer face à des challenges économiques.
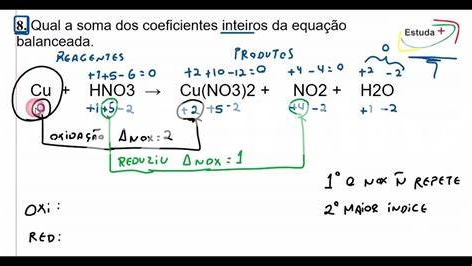
Modéliser Des Phénomènes Naturels Avec Des Équations
Dans le monde naturel, les équations quadratiques sont des outils puissants qui permettent d’appréhender une multitude de phénomènes. Par exemple, lorsqu’on cherche à comprendre l’arc de trajectoire d’un projectile, il est essentiel d’enregistrer l’équation et ses variables clés pour déterminer l’impact de la gravité et la résistance de l’air. En prenant pour exemple le mouvement d’une balle lancée dans les airs, il est possible d’encontre a equação quadrática com coeficientes inteiros sabendo que suas raízes são, ce qui nous aide à prédire où et quand la balle touchera le sol. Ces analyses nous permettent aussi de faire des prévisions sur des événements environnementaux, comme les crues d’une rivière identifiées à travers des modèles graphiques et des simulations informatiques.
Au-delà de cette application, les chercheurs en biologie utilisent des équations quadratiques pour modéliser la dynamique des populations. Dans ces contextes, certaines espèces peuvent exiger des ressources limitées, incitant à une analyse plus complexe des interactions entre espèces, ce qui souvent aboutit à des formulations quadratiques. De même, en chimie, la réaction entre différentes substances peut parfois être modélisée à l’aide d’une équation carrée, établissant un lien entre les concentrations des réactifs et des produits. Ainsi, que l’on se penche sur les lois de l’optique ou sur les cycles de vie d’un organisme, le recours à ces équations devient vital pour recueillir des données exploitables et améliorer nos connaissances.

Analyser Des Courbes De Croissance En Biologie
Au cœur de la biologie, l’analyse des courbes de croissance permet de mieux comprendre les dynamiques des populations et les interactions entre les espèces. En prenant, par exemple, celles des bactéries, on peut observer une phase exponentielle suivie d’un plateau. L’équation quadratique peut alors surgir pour modéliser des aspects tels que lorsque les ressources sont limitées, illustrant ainsi l’importance de la suture entre théorie et pratique. Dans ce contexte, il est possible de rencontrer une équation quadratique avec des coefficients entiers sachant que ses racines sont liées à des taux de croissance spécifiques.
Cet outil mathématique ne se limite pas seulement aux microbes. En écologie, les modèles de croissance des plantes ou des animaux peuvent aussi être représentés à l’aide d’équations quadratiques. Cela peut aider à prédire les effets d’une compétition pour les ressources ou d’un changement climatique. De plus, en examinant ces courbes, les chercheurs peuvent déceler les signaux de perturbations dans l’environnement. Ces analyses sont parfois aussi précieuses que des *Happy Pills* pour les biologistes, leur fournissant des éclaircissements sur les mécanismes d’adaptations des espèces.
En conclusion, qu’il s’agisse de microbes, de plantes ou d’animaux, l’analyse et la modélisation des courbes de croissance présentent des avantages nettes pour la compréhension des phénomènes biologiques. En employant des outils mathématiques comme les équations quadratiques, les scientifiques peuvent élaborer des stratégies de gestion des ressources naturelles. Cela renforce indéniablement l’idée que la biologie n’est pas qu’une série d’observations, mais un ensemble complexe d’interactions qui peuvent être mesurées, analysées et prédictivement modélisées.
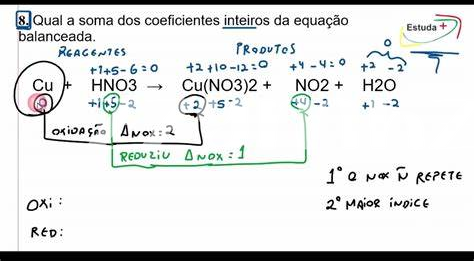
Optimiser Des Ressources Dans Des Projets D’ingénierie
Dans le monde de l’ingénierie, l’utilisation des équations quadratiques se révèle être essentielle pour améliorer l’efficacité des projets tout en maîtrisant les coûts. Prenons, par exemple, le cas d’un projet de construction d’un pont. En identifiant les contraintes et les ressources disponibles, les ingénieurs peuvent rencontrer une équation quadratique avec des coefficients entiers, sachant que ses racines sont liées aux différents matériaux utilisés et aux forces en jeu. En modélisant ces paramètres à l’aide d’une équation, ils peuvent déterminer la manière dont ces ressources doivent être allouées pour garantir la stabilité et la durabilité de la structure, réduisant ainsi le gaspillage et optimisant le projet.
De plus, les ingénieurs utilisent souvent des simulations pour visualiser l’impact de différentes configurations sur le budget global. Ces analyses sont cruciales, surtout lorsque des délais “Stat” doivent être respectés. La recherche du juste équilibre entre le matériau, le coût et le temps de réalisation peut être facilitée par des outils mathématiques basés sur des équations quadratiques. Par ailleurs, dans certaines situations, les décisions peuvent impliquer des calculs complexes qui, sans l’utilisation de ces équations, prendraient beaucoup plus de temps à établir. Au final, la maitrise de ces concepts mathématiques ne fait pas que soulager le “pill burden” associé à la gestion de projets, mais elle pousse également à l’innovation au sein des équipes d’ingénierie.
| Paramètre | Valeur |
|---|---|
| Coût des matériaux | 100 000 € |
| Délai de construction | 6 mois |
| Durabilité | 50 ans |
Utiliser Les Équations Pour Prédire Des Événements Futurs
Les équations quadratiques jouent un rôle essentiel dans la prévision d’événements futurs, en particulier dans des domaines tels que la finance, la physique et même l’écologie. Par exemple, en économie, ces équations permettent d’anticiper les tendances du marché et d’évaluer les impacts des décisions financières. En utilisant ces outils mathématiques, les investisseurs peuvent calculer des projections de bénéfices ou de pertes, leur permettant de prendre des décisions plus éclairées. Cela est particulièrement vrai lorsque les économies fluctuent rapidement, exigeant une analyse rapide, souvent appelée “stat”.
De plus, dans le domaine de la santé, la prévision d’événements peut être cruciale. Les chercheurs utilisent des modèles quadratiques pour évaluer l’impact potentiel de nouveaux traitements. En analysant les données sur les ‘happy pills’ ou d’autres médicaments, ils peuvent prédire comment une population réagira aux traitements, affaiblissant ainsi les risques d’effets secondaires groupés, souvent qualifiés de “side effects”. Grâce à la modélisation, une compréhension approfondie des interactions médicamenteuses émerge, facilitant la prescription d’un ‘cocktail’ de médicaments adaptés.
Finalement, la capacité à prédire des événements futurs s’étend dans des domaines comme la biologie, où les chercheurs utilisent des équations quadratiques pour modéliser la dynamique des populations et des écosystèmes. En tenant compte des variables environnementales et des comportements des espèces, ces équations peuvent offrir un aperçu précieux sur l’évolution d’une espèce ou d’un écosystème. En somme, la puissance des équations quadratiques transcende le simple cadre mathématique, se transformant en un outil indispensable pour la compréhension et la prévision dans divers domaines.